I studied stochastic processes as part of my master’s degree, but that was a while ago and I’ve forgotten a lot, so when I saw a Stastical Mechanics course appear on Coursera I couldn’t resist. The first week covers some methods (albeit inefficient) for calculating 𝛑.

Direct sampling Monte Carlo

1
2
3
4
5
6
7
8
9
10
11

function mc_pi(N)
    n_hits = 0
    for i = 1:N
        x = rand() * 2 - 1
        y = rand() * 2 - 1
        if x^2 + y^2 < 1
            n_hits += 1
        end
    end
    4 * n_hits / N
end

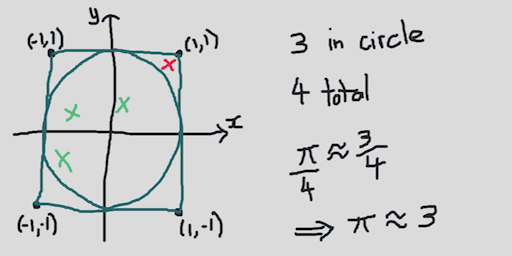
This picks an (x, y) coordinate in the rectangle bounded by x=-1, x=1, y=-1, y=1 N times. Each time, we check if the point lands in the unit circle. The ratio of the areas of the circle and square is 𝛑/4, so we can use 4 * n_hits / N to approximate 𝛑.

Markov chain Monte Carlo

This example doesn’t highlight the weaknesses of direct sampling, but if we are dealing with non-rectangular regions or higher dimensional spaces, it is less practical to implement. In these cases a random walk walk may work better (although I’ll stick to a 2D squares for simplicity in my examples).

Rather than sampling points directly, we pick a sequence of points via a random walk; these either fall inside or outside of the unit circle and can then be used to approximate 𝛑. However, there is a possibility that the random walk may take us outside the sampling region, and the algorithm has to deal with it appropriately.

Here is the algorithm demonstrated in the Coursera class, translated into Julia. I was pretty surprised when I saw it…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function markov_pi(N, delta)
    x, y = 1.0, 1.0
    n_hits = 0
    for i = 1:N
        del_x = (rand() - 0.5) * 0.5 * delta
        del_y = (rand() - 0.5) * 0.5 * delta
        if (abs(x + del_x) < 1.0) && (abs(y + del_y) < 1.0)
            x, y = x + del_x, y + del_y
        end
        if x^2 + y^2 < 1
            n_hits += 1
        end
    end
    4 * n_hits / N
end

When the walk lands at a point that is “out of bounds”, it simply pretends that our marker hasn’t moved, but it still counts that as one iteration of the sequence. So that point is counted twice, or even more if it goes out of bounds again! (Gasp)

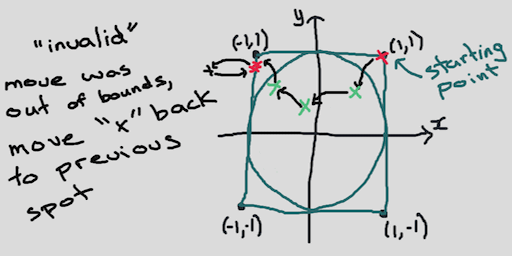
This really confused me for a few minutes, but I had a flash of intuition – helped by the lectures, of course :)

When we land near an edge position there is a chance we will stay there, but this is conditional upon us landing there in the first place. Conveniently, the chance that we move out of bounds and remain at the same spot precisely counteracts the reduced probability of landing near the edges.

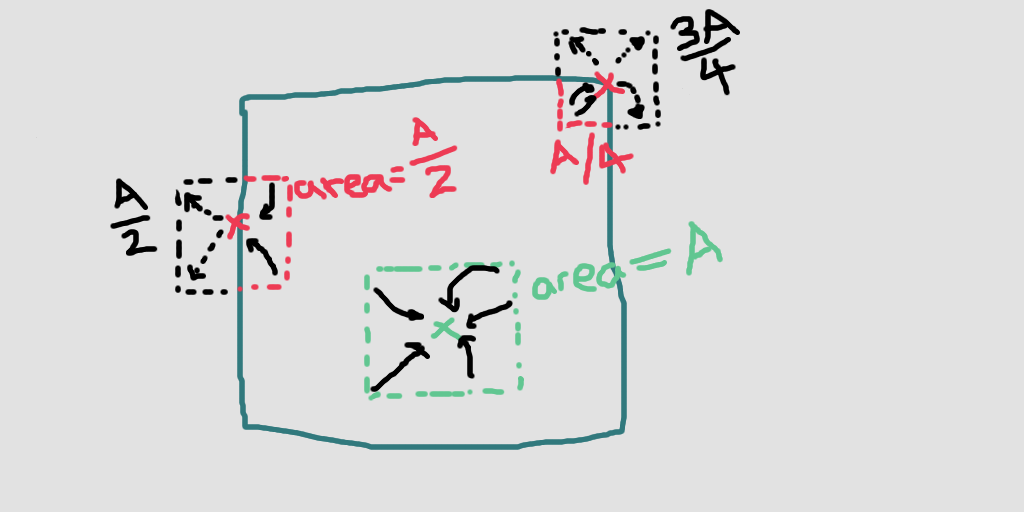
The green point in the center has a “catchment area” of A, but upon landing, we move to a new spot with probability 1. The point on the left side has half the catchment area, however, if we land there we expect to stay for one extra move (½ + ¼ + 1/8 + …). Similarly, the point in the top right has ¼ the catchment area, but if we land there we expect to remain for an extra 3 moves (¾ + 9/16 + 27/64 + …).

As mentioned in the title, this was a pretty handwavey explanation, but I was impressed that such a simple algorithm corrects its own “flaws”. A more detailed explanation can be found in Wikipedia.

One of my aims for 2014 is to improve my grasp of concurrency. I’m hoping to write concurrent programs using a various approaches (threads, async, channels) and take the Pattern-Oriented Software Architectures Coursera class which looks into these issues in the context of distributed systems.

With this in mind, when I decided to take my Github Data Analysis project and work on version 2, the first thing I decided to do was restructure the API scraper to handle multiple concurrent connections.

There are a few approaches for concurrent programming in Python, and the async framework Twisted gets a lot of love at Hacker School, but I decided to stick to the standard library and use the threading module following this IBM tutorial. (Async support for the standard library is being worked on currently.)

The gist of the tutorial was to use queues to pass data between threads using a producer-consumer model. The main thread loads the initial URLs (users) into download_queue and 30 FetchUrlWorker threads take the URLs from the queue and fetch the data. The necessary data is added to db_queue and other URLs (repository and contributor listings) are added to download_queue. The single DbWorker thread collects the data from db_queue and inserts it in a SQLite database. The program ends when both queues are empty.

The producer consumer model isn’t too hard to understand but I had a few issues getting it to work smoothly:

• If an error causes a task to not be indicated as complete the queue will not empty and the program hangs. I ended up resorting to Pokémon exception handling to ensure that self.download_queue.task_done() was always called.
• Ctrl-C doesn’t work as expected, it refuses to close child threads in case they are in the middle of something critical. This was a real nuisance when I was dealing with non-empty queues and the program was hanging. I hope to experiment with catching the KeyboardInterrupt exception in the main thread and setting variable that is checked by the loop in the other threads to tell them to halt.
• Thread objects are initialized in the main thread, not the child thread that they create. I was using a sqlite.Connection object which can only be used in one thread by default. Initializing it in DbWorker.__init__ (executed in the main thread) and using it in DbWorker.run (executed in the child thread) raised an exception and it took me a while to work out what the problem was.

While it may not be my finest code I’m pretty happy with how it has turned out so far, it runs far faster than the single threaded version and the producer-consumer model is conceptually simple even if dealing with the edge cases requires some care. I’ve been dabbling with node.js recently and I’ve been reading about Twisted so I should have something to compare this approach with soon!

I started messing around with literate programming in Racket recently using the Scribble tool. I had a little trouble getting the basic example working, because you need a base Scribble document in addition to the literate program file:

1
2
3
4
5
6
7

#lang scribble/base

@(require scribble/lp-include)

@title{Fizzbuzz in Literate Racket}

@(lp-include "fizzbuzz.scrbl")

Once this template is set up the main program can be written in fizzbuzz.scrbl:

1
2
3

#lang scribble/lp

...

Finally, to compile with cross-reference links correctly it is necessary to use, scribble +m --redirect-main http://docs.racket-lang.org/ index.scrbl. As +m links against local documentation by default --redirect-main is used to point to the main racket site.

Here’s the final output.

One of my first interviews post-Hacker School was with HuffPo Labs, I particularly enjoyed it because of the off-the-wall programing challenge they gave me. Many of you will have heard of brainfuck, though I doubt as many of you will have actually programed in it. The HuffPo Labs guys asked me to write a few simple programs in the language and afterwards I wrote a simple interpreter.

The rather terse syntax makes reading brainfuck programs difficult, but the other challenges of programing in the language can easily be explained in a more familiar format. The Wikipedia article provides a direct translation of brainfuck to C, but I’m going to use a C-like pseudo code in this article.

Basic operations

Brainfuck has a “tape” of data, which we can think of as an array or linked-list that’s infinite in both directions. Like a linked-list we can only move left or right one cell at a time, we can’t “jump” to an arbitrary point in the tape. We also have the ability to increment or or decrement the current byte by 1. Treating the tape as an array, data[], indexed by i, the following operations are permited:

1
2
3
4

i++; // move the data pointer one to the right
i--; // move the data pointer one to the left
data[i]++; // increment the value at the data pointer
data[i]++; // decrement the value at the data pointer

As a result even simple changes to the data require multiple instructions. It is assumed that we start at i = 0, so to add three to the byte stored at data[2] we need to do the following:

1
2
3
4
5

i++;
i++;
data[i]++;
data[i]++;
data[i]++;

In addition brainfuck allows us to read a single byte into the current place in memory, and output the value of the current byte in memory.

1
2

data[i] = input()
output(data[i])

Finally, brainfuck has a single control structure, equivalent to a while loop that runs while the current data value is non-zero.

1
2
3

while (data[i] > 0) {
    ...
}

Count down

The “hello world” of brainfuck takes a single byte as input and counts down to zero printing each number in turn. This only requires a single data cell to be used, so we don’t need to move the data pointer at all.

1
2
3
4
5
6

data[i] = input();
while (data[i] > 0) {
    print(data[i]);
    data[i]--;
}
print(data[i]);

Counting up

Since these loops only terminate when data[i] equals zero, other types of loops have to be shoehorned into this format. To loop upwards we have to use a second data cell: data[0] holds the loop variable which we decrement and data[1] holds a byte which we increment and output.

1
2
3
4
5
6
7
8
9
10

data[i] = input();
while (data[i] > 0) {
    data[i]--;
    i++;
    print(data[i]);
    data[i]++;
    i--;
}
i++;
print(data[i]);

If-Else

This didn’t come up in the interview but I felt I should try it on my own as if-else is a fundamental control structure of most programing languages. Producing an if-else with arbirary predicates seemed a little too ambitious so I set myself the following target: Take one number as input, print 1 if it’s non-zero and 0 otherwise.

The construction I came up with uses nested while loops and two data bytes. The “equals zero” case is simple, if the input is zero then the first while loop doesn’t execute and the default value of zero is return from the second byte. If the input is non-zero then both while loops execute, the inner loop reduces data[0] to zero, ensuring that both while loops terminate, and the outer while loop increments data[1] before terminating.

I’ve written it here with named variables, in = data[0] and out = data[1], for easy reading:

1
2
3
4
5
6
7
8
9

in = input();
out = 0;
while (in > 0) {
    while (in > 0) {
        in--;
    }
    out++;
}
print(out);

It’s then easy to replace in, out with data[i] and intersperse these with i++s and i--s to move the data pointer back and forth.

1
2
3
4
5
6
7
8
9
10
11

data[i] = input()
while (data[i] > 0) {
    while (data[i] > 0) {
        data[i]--;
    }
    i++;
    data[i]++;
    i--;
}
i++;
print(data[i]);